The Physics of Moving a Bike
If we are going to use power data to guide our training and racing, it helps to know a bit about the role of power in moving a bike. Once you understand a bit more about how power does – or doesn’t – make you faster, you can use your power meter to make better decisions about how to equip and sit on your bike. You will also better understand the pacing advice given on this site.
The only thing keeping your bike from going infinitely fast on flat ground is drag (well, except for general relativity, but we don’t go that fast). Drag is a force that pushes backwards along your line of travel. Your bike is subject to three principal sources of drag:
• Mechanical drag, in the form of friction from the bearings and the chain;
• Tire drag, or rolling resistance, caused by the constant squashing of the tire against the road; and
• Aerodynamic drag, or wind resistance.
Of these, the largest is wind resistance. But even the other two are worthy of your attention when fitting out your bike.
Mechanical drag is pretty much a small, fixed number. It hardly varies from bike to bike. Even the new fancy ceramic bearings do very little to make an appreciable dent in mechanical drag. The chain is the biggest source of friction, and there haven’t been any advances in chain technology in 100 years. The roller chain is remarkably efficient. The only major new drivetrain technology affecting friction in recent years is the new trend of outboard-mounted oversized bottom bracket bearings. Perversely, these fancy new bottom brackets have significantly higher drag than the simple ones they replaced! Basically, the main thing you can do to minimize drivetrain friction is to keep your wheel hubs properly maintained and your chain oiled. Then, forget about it and move on to more important things.
Next up is tire drag. A pneumatic (air-filled) tire has a flat spot where it touches the ground – the contact patch. About half your weight is on each tire, making an oval flat spot a little less than one square inch in size. As the tire rolls forward, the leading edge of the contact patch moves around the tire. Some rubber that used to be round is bent and flattened. As that spot on the tire leaves the back end of the contact patch, it bends back into its favored round shape. That bending and un-bending action doesn’t happen freely – it involves friction within the tire. That little bit of friction, happening constantly and rapidly, adds up and slows the bike down.
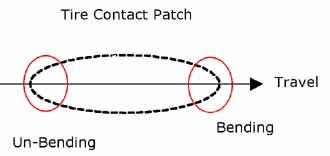
Now, before you go thinking that pumping the tire up really hard will reduce this drag, you need to consider bumps in the road. It is true that high pressure tires can minimize the bending and unbending friction, but they do so at the cost of bouncing over tiny bumps in the road instead of “squishing” over them. Every bumpy bounce causes the bike to divert some of its kinetic energy into an up-and-down direction instead of forward, and that energy is effectively lost. So, a nicely rolling tire needs to strike a balance between being pumped up enough to minimize the contact patch drag, and not so much as to have it losing speed to the tiny constant bumps encountered on normal asphalt.
The answer to this little optimization problem is found by tire testing. Cutting to the chase, the answer is: For racing on normal public roads, you should pump your tires to between 100 and 120 pounds. Just because the tire might have “190psi” printed on the side of it doesn’t mean you should do it! That is a maximum number printed for your protection, and would apply only if you were racing on a track.
There is an equation for calculating the drag that the tires impart to the bike. For our purposes, it is convenient to express that drag force in terms of watts:
Watts to overcome tire drag = Crr*M*g*V, where
Crr = Coefficient of Rolling Resistance (determined by testing the tire)
M = Mass of bike plus rider (plus 4 water bottles, 2 tubular spares, a Bento box, gels, a Salt Stick and a tool kit).
g = The acceleration due to gravity, 9.8m/s^2 (remember high school physics!)
V = The ground speed of the bike.
Since M is nearly fixed, and g is most certainly fixed, you can see that tire drag varies directly with Crr and with bike speed. If you go twice as fast, you use up twice as many watts overcoming tire drag. Since you want to go as fast as you can, the sole variable left under your control is the Crr of your tires.
This is an example of how power meters are changing things. Just as the Internet gave ordinary folks easy and direct access to data and information, power meters allow us to get direct answers to questions that had previously been almost impossible to get. Until the last couple of years, you bought tires because the guy at the bike shop said they were fast. How did he know they were fast? Because his fast buddy rides them, and so do a bunch of pros. Heck, if the pros go fast on them, they must be fast, right? I had a bike shop guy insist that a particular brand of tires was fast because the shop sold a lot of them. “We wouldn’t sell a lot if they weren’t fast!” I since discovered via my own testing and that of friends that this tire is about the slowest thing you can buy.
The Crr of a name-brand racing tire will range from 0.004 to 0.007. At a glance, those numbers look like they are close together, and you can buy highly regarded and expensive tires at both ends of that spectrum. However, let’s do a little math, using my current chubby out-of-shape self as an example.
Crr = 0.004 or 0.007
M = 87 kilograms
g = 9.8m/s^2
V = 8.94 m/s (20 mph)
Rolling along at IM bike pace, I am expending either 30.5 watts or 53.4 watts to overcome tire drag. Which would you prefer? This difference of 22.9 watts represents – are you sitting down – about 12-13 minutes in an Ironman bike ride!
Until the recent widespread use of power meters allowed curious hobbyists to test tires for themselves, very few people had any inkling of the huge difference between highly regarded tires. Another tradition-shaking outcome of this new testing is that tubulars are not, as a class, faster than clinchers. The vast majority of tubular tires are significantly slower than their high-quality clincher counterparts. Only the very best tubulars, glued in a fashion that will not permit a quick road-side tire change, are as fast as the best clinchers.
Wind resistance
The largest drag force on a bike rider going at racing speeds is wind resistance, or aerodynamic drag. As you roll along, air molecules are slamming into you. Sure, each one is pretty light, but they add up!
The kinetic energy of an air molecule increases with the square of its velocity. A molecule that hits you going twice as fast imparts four times the energy. The equation for the drag force experienced by a cyclist is:
Aerodynamic Drag Force = ½*(air_density)*CdA*V_wind^2, where
Air_Density = A constant that depends on temperature, humidity and pressure (or altitude). A normal figure for sea-level riding is about 1.22. The figure will drop in higher altitudes or in humid conditions.
CdA = The Coefficient of Drag times the Frontal Area (Cd*A). While this is technically two separate terms, we usually use a single figure since it is difficult (and unnecessary) to determine the two individual pieces in wind tunnel or field testing. The Cd part tells us how easily air slips around an object; the A part tells us how big the object is. The product of the two is where the action is.
V_wind = The effective wind velocity the cyclist experiences, in the forward direction. While the wind might be coming at you from the side or the back, it is only the effective headwind that slows you down.
CdA is directionally dependent. In other words, the CdA of a cyclist from the front is different than the CdA from a slight angle. We care about the CdA from the front, and you will sometimes see this stated as “CxA” to denote that we mean “along the line of travel “x”.”
The effective wind velocity will depend on how fast you are going, and on the ambient wind. If you are traveling 25 mph down the road, with a 5 mph tailwind, your V_wind is 20 mph. If there was a headwind of 5 mph, your V_wind would be 30 mph. In crosswinds, you need to brush up on your trigonometry to figure it out.
The drag force is important, to be sure, but we are here to talk about power. Power is the product of force and velocity. But, what velocity do we use – the road speed or the effective wind speed? In this case, we use road speed. The speed of the wind in your face determines the drag force; the speed at which we drive the bike determines how much power it takes to overcome that drag force. Multiplying the above equation by road speed, we get:
Power to Overcome Wind Resistance = ½*(air_density)*CdA*V_wind^2*V_road.
In any conditions with ambient wind, these two velocity terms will not be the same. Naturally, they are related since increasing road speed will increase the headwind. We can solve the equation for any given situation.
When dealing with wind, you can’t control the air density or the ambient wind. Since you want your road speed to be as high as possible, the only variable left under your control at a given power output is your CdA. CdA can be managed via bike equipment, clothing and rider positioning.
Bike equipment that has been demonstrated to reduce CdA includes deep-rimmed and disc wheels, wheel covers, aerodynamic framesets and forks, and handlebars that present a low profile to the wind. These components can reduce both the Cd and the A parts of the CdA figure.
A bike rider can reduce her CdA by wearing tight-fitting clothing. Anything that flaps in the wind increases CdA. An aerodynamically designed racing helmet can make a significant improvement in CdA as it makes the rider more streamlined, lowering the Cd.
Finally, the rider’s position on the bike is the single largest determinant of CdA. If you sit up straight, your CdA will be high. If you bend over and tuck your chin down into your chest, your CdA will be lower.
The CdA of the combined bike and rider in a triathlon can fall into the range of about 0.25 to 0.33. I will note that very few people get as low as 0.25; the fat part of the bell curve seems to be in the 0.28-0.31 range and plenty of folks are over 0.33. Running a few examples…
CdA = 0.28 or 0.31
V_wind = 20 mph
V_road = 20 mph (ie, a calm day)
Air_dens. = 1.22
The power to overcome wind resistance at 20 mph on a calm day can be either 122 watts or it can be 135 watts, in this example. That is 13 watts difference, equating to about 8 minutes in an Ironman for an AG racer. Just what is the difference between a rider with a CdA of 0.28 and another with 0.31? Probably nothing you can see by just looking at them. One might or might not “appear” any more aero than the other. They could have identical bikes and equipment, and fitness, and be coming into T2 eight minutes apart simply because one tucked his head down for 6 hours. If they do happen to come into T2 together, one twin will have ridden 13 watts harder, and will be easily outrun by his buddy.
Without specific and careful testing, it is hard to know for sure whether two similar positions have a similar CdA.
Contrary to a bit of conventional lore, you don’t need to be fast to benefit from lowering your CdA. In fact, the slower you are, the more time you save by a given amount of CdA reduction. A deep-rimmed front wheel might be good for Chris Lieto, but it is really good for you and me.
Another thing you might note from this article is that, while cyclists tend to not think much about tires, the choice of tires can have a bigger effect on saving time than does the selection of aero bike gear or bike positioning.
You might also note the role that weight plays in these equations. The total bike and rider mass enters the equations in just one place (tire drag), and its effect is multiplied by speed. CdA, on the other hand, is multiplied by speed raised to the third power. In a sense, reducing your CdA is three orders of magnitude more important than saving weight when on flat ground.
The mention of weight leads us to the final part of the physics of propelling your bike – gravity.
Gravity and You
The final bit of physics that conspires to slow you down is gravity. After doing your best to keep your bike moving by overcoming tire, wind and friction drag, you have added a bit of kinetic energy to your bike. As soon as you start going upwards, that kinetic energy starts to become converted to potential energy. Less of it is available to keep the bike moving, and you slow down. Riding up a hill requires additional work that is equivalent to that required to lift the bike directly up the height of the hill. Any work spent lifting is not available for driving forward.
The power required to move your bike up a given grade, ignoring the other three forms of drag, can be calculated with the following equation:
Power to Lift the Bike up a Hill = M*g*[sin(arctan(slope))]*V_road, where
V_road = Road speed, as before
M = Weight of bike and rider and gear
g = The gravitational acceleration (9.8)
sin(arctan(slope)) = The sine of the arctangent of the road slope
slope = road slope, expressed a percentage: rise divided by run. A road that rises 6 feet for every 100 feet of horizontal travel is a 6% slope.
The multiplication of the V_road and sin(arctan) terms together essentially spits out the velocity in the vertical direction – how fast you are lifting the bike. The rate of lifting, times your weight, times the gravity constant…gives you the power required to lift the bike. Again, that power is used up and is not available to drive the bike forward.
Riding up a 4.5% slope at 200 watts will net me around 10 mph. About 170 of those watts are being used in lifting me up the hill; only 30 watts are moving me forward.
Now for the fun part – rolling over the top. If all those 200 watts didn’t go into driving me forward, where did they go? Energy is conserved, right? You bet – those extra watts got stored up as potential energy. When you begin to coast downhill, you pour out that stored gravitational potential energy. On that 4.5% grade, I am going to coast up to about 30 mph if I just stay in the same sitting-up position on my bike with a CdA of 0.31 (I’m a timid descender). I’m producing zero watts, but what is going on in total?
Gravity is doing all the work for me – producing about 530 watts! That’s the wattage requirement for traveling at 30 mph and overcoming wind and tire drag. Every watt you spend getting up the hill is returned to you coming back down. However, there is a catch. You don’t get the time back, only the power. The reason is that you went up slow and lost very little power to the wind. When you come back down fast, you lose lots of power to the wind. So, while the total energy and power is preserved riding up and coasting down, you lose time in the hills because of wind resistance.
Why do hills slow us down? Aerodynamics. At a given bike + rider weight, and with a given amount of fitness, the fastest way up and down a hill is to have good aerodynamics. That’s an interesting twist, eh?







Start the discussion at forum.slowtwitch.com