Why Wheel Aerodynamics Can Outweigh Wheel Weight and Inertia

When talking about bicycle wheels, their weight typically receives a lot of attention. This is true for a couple of reasons: First, obviously weight of any sort in bicycle parts receives attention, especially for courses with significant uphill sections, and secondly, most people remember from their high school Physics classes that rotating mass also results in rotational inertia, or a resistance to "spin up". The common wisdom is that wheel mass, since it is rotating, counts "doubly bad" as compared to non-rotating mass. There's a grain of truth to this common wisdom, but it doesn't tell the entire story. In fact, in most cases, wheel mass and rotational inertia tend to be exceedingly small determinants of a particular wheel's performance; much less than the effects of the wheel's aerodynamics, or a particular tire's rolling resistance. If you read most wheel reviews however, there's nearly always a reference to the wheel weight, and in some cases certain reviewers have spent time and money constructing devices to compare wheel inertias and have used that as a main property to rank the wheels against one another. In the example I show below, you'll hopefully begin to see why these sorts of rankings of inertia are actually concentrating on a wheel property that has only a minor affect on wheel performance in the context of the overall bike+rider "system."
Here's the example: I took an actual acceleration of mine from a race file. In this case it was an attack to go for a mid-race prime on a flat section of a crit course. In the span of 5s I accelerated from 25.5 mph to 30.4 mph with an average of 766W expended over those 5s (1s peak of 1080W). Although that's just one of my lowly Cat 4 examples, I think that it's representative of a fairly significant acceleration effort and would be a "worst case scenario" for any wheel inertia effects.
So, I took a look at what the peak forces at the pedal (assumed to be ~2X the average pedal force around the crank cycle) would need to be to create that acceleration due to the different "loads," i.e. merely accelerating the mass, overcoming the increase in aero drag, and also overcoming the increase in rolling resistance with velocity. I then took a look at what a difference in mass of 400g would mean to the situation. It's a somewhat simplistic look at it, but here's how it broke down:
- Increase in peak force (average over 5s) at the pedal just to accelerate the mass of myself plus the bike = 58.6 lbf. (this is the average ABOVE what it took to go steady state at 25.5 mph).
- Increase in peak force at the pedal to overcome increased aero drag at end of 5s span = 14.7 lbf.
- Increase in peak force at the pedal to overcome increased rolling resistance at end of 5s span = 11.5 lbf.
- Increase in peak force (average over 5s) at the pedal if mass above is increased by 400g = 0.3 lbf.
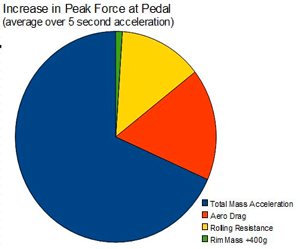
As you can see, the increase in peak force at the pedal (basically, what you would "feel") is swamped by the total of the other forces…you aren't going to be feeling that mass increase in an acceleration. I even looked at what it would mean if ALL of that 400g increase was at the extreme outer edge of the rims and it's effects on the rotational inertia and the additional force needed to "spin up" that additional mass. Doing that changes that last bullet from 0.3 lbf to 0.9 lbf…3X worse, but still minuscule in the grand scheme of things.
As can be seen in the pie chart to the left, the vast majority of the increase in peak force felt at the pedal was due to just linearly accelerating my (and my bike's) mass. Additionally, the increases in aero drag and rolling resistance accounted for approximately 1/3 of of the total increase in peak pedal force. The effect of increasing the rim mass of the wheels by nearly a full pound (400g) resulted in an increase in the average peak pedal force over the 5s acceleration of just 1%…in other words, an amount not likely to be "felt" at the pedals. It's pretty clear which areas of wheel performance the most benefit can be gained from making improvements: in the aerodynamics of the wheels and the rolling resistance of the tires and tubes applied to them.




Start the discussion at forum.slowtwitch.com